| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- Spark
- datahub
- bitcoin
- 디스코드챗봇
- embodied
- frontend
- data discovery
- GPT
- vision-language navigation
- databricks
- ChatGPT
- airflow
- 챗봇
- embodied ai
- backend
- 블록체인
- s3
- blockchain
- video understanding
- Golang
- Rust
- MLFlow
- vln
- 디스코드
- bricksassistant
- Ai
- crwaling
- discord
- 디스코드봇
- Hexagonal Architecture
- Today
- Total
BRICKSTUDY
Supervised Learning 기초 본문
0. 개요
안녕하세요. 브릭스터디 박찬영입니다. 이번 포스팅은 요새는 모르는 사람이 없는 Machine Learning, Deep Learning의 학습 Method인 supervised learning에 대해서 이야기를 해보려고 합니다. 많이 배운 내용들이지만, 자주 잊어버리는 내용들이라고 생각해서 공유하면서 남기려고 합니다.
1. Setting
Supervised Learning (지도학습)이라고 하는 학습 메커니즘은 현대 AI에서 가장 많이 사용되는 방법이 아닐까 싶습니다. 우리가 어떤 image로부터 해당 이미지의 object 카테고리를 예측하는 모델을 만든다고 했을 때, 모델이 잘 예측할 수 있도록 "연습"을 시키는 행위라고 볼 수 있습니다.
(문제 - 정답)으로 구성된 데이터를 모델이 보면서 연습할 수 있도록 하는 것
지도학습의 setting을 가볍게 정리하면 다음과 같이 작성할 수 있습니다.

주어진 데이터로부터 출력 y를 추정하는 함수의 가중치를 학습한다.
즉, Data로부터 가중치(지식, Representation)을 학습한다.
Prediction is difficult

label 자체를 predict하는 것보다 해당 Input이 특정 label에 속할 "확률"을 예측하는 것이 불확실에 대해서 더 유용하게 사용될 가능성이 있습니다.
가령 이런 경우를 생각해볼 수 있을 텐데, 손글씨 숫자 4 image를 보고 모델이 예측을 수행했다고 생각해 봅시다.
그림처럼 모델이 "이 image는 4일 확률이 90%야!" 라고 하는 경우도 있겠지만, 굉장히 애매한 숫자를 봐서 "아 이 image는 4일 확률이 51%고, 9일 확률이 49%야"라고 했을 때, 둘 다 label 자체를 예측했다고 하면, "4"라는 결과를 낼 겁니다. 그렇지만, 후자의 경우에는 모델의 출력에 대한 confidence가 굉장히 낮습니다.
만약 label 자체를 예측했다면 이러한 불확실성에 대한 정보를 알 수가 없기 때문에, probability를 예측 하는 것이 합리적인 방식이라고 생각할 수 있습니다.
Predicting Probabilities
- Make more sense than predicting discrete labels
- Easier to learn due to smoothness
Conditional Probabilities
더 디테일한 내용을 살펴보기 전에 잠시, 조건부 확률에 대한 개념을 잡고 넘어가 봅시다.


두 확률변수에 대해서 우리는 chain rule, conditional probability를 정의할 수 있습니다.

우리가 생각하는 모델은 결국 x가 주어졌을 때 y를 출력하는 "어떤 함수"라고 생각할 수 있고, 이 함수를 x가 주어졌을 때, y에 대한 조건부 확률 분포라고 생각할 수 있습니다.
데이터 input x가 주어졌을 때, y의 확률분포를 알면 특정 x가 주어졌을 때, 출력 y의 확률값을 알 수 있음.
2. How do we represent P(Y | X)

그림과 같이 object probability를 출력하는 프로그램을 작성한다고 할 때, 중요한 포인트는 확률의 조건을 만족하는 것입니다.
여기서 확률의 조건 2가지를 생각해 볼 수 있습니다.
확률의 조건
1. Positive
2. Sum to 1
프로그램을 다음과 같이 작성했다고 해봅시다.
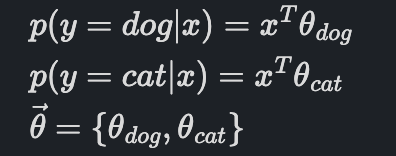
이렇게 작성하면 어떤 문제가 발생할지 생각해 봅시다. 이렇게 프로그램을 작성하면, 확률의 조건을 만족하지 않습니다.

그러면 이번에는 프로그램 자체를 이렇게 바꿔봅시다.
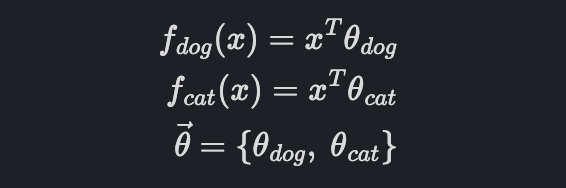
여기서 f는 어떤 확률분포가 아니기 때문에 조건을 만족할 필요가 없습니다.
아까는 확률을 예측해야 한다면서 왜 갑자기 그냥 function으로?
끝이 아니라, 이제 이 함수 f들을 이렇게 만들어서 조건부 확률로 만들어봅시다.
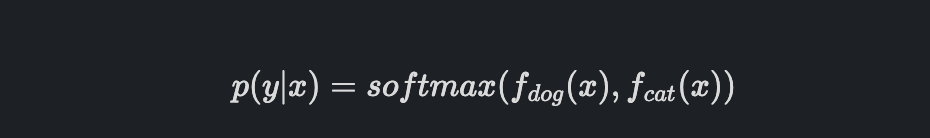
이렇게 표현하면, p(y | x )는 positive condition, sum to 1 condition 모두 만족할 수 있어서 valid 한 probability distribution이 되는 것입니다.
우리가 많이 쓰고 있었던 softmax function을 쓰는 이유를 이제 알 수 있을 것 같습니다. 사실 이론상 softmax function 뿐만 아니라, positive 하고 sum to 1 인 어떠한 함수든 사용할 수 있습니다.
How to make number "z" positive?
우리가 어떤 숫자 z를 어떻게 positive 하게 만들 수 있는지에 대한 몇 가지 방법을 살펴봅시다.
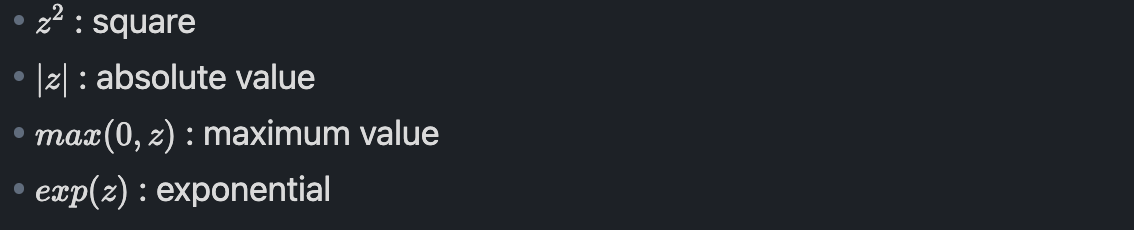
이러한 방법은 어떤 숫자든 positive하게 만드는 간단한 방법들입니다.
특히 exp(z)는 one-to-one, onto function이기 때문에 더욱이 편리한 방법이다.
How to make a bunch of numbers sum to 1?
여기서는 Normalization이 대표적입니다. 각 값을 전체 값의 합으로 나누면(전체에서 차지하는 비율로 표현), 각 값들을 더 했을 때, 합이 1이 됩니다.
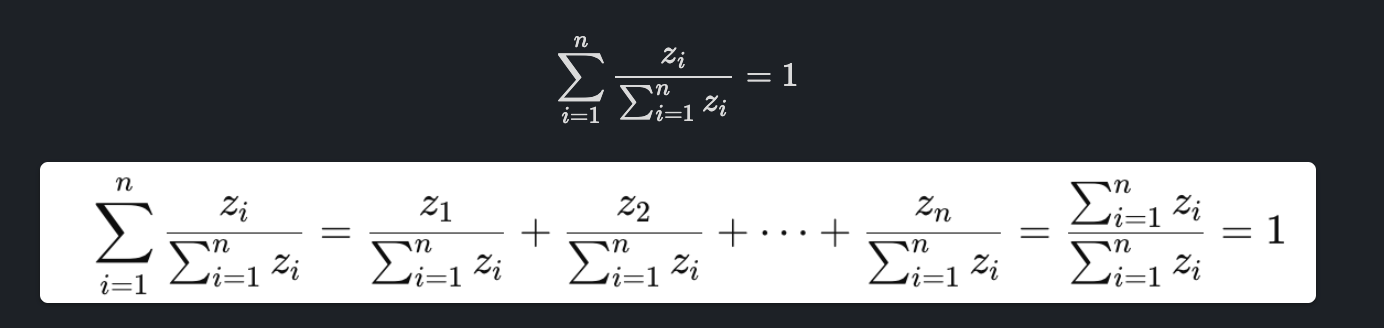
Define Softmax function
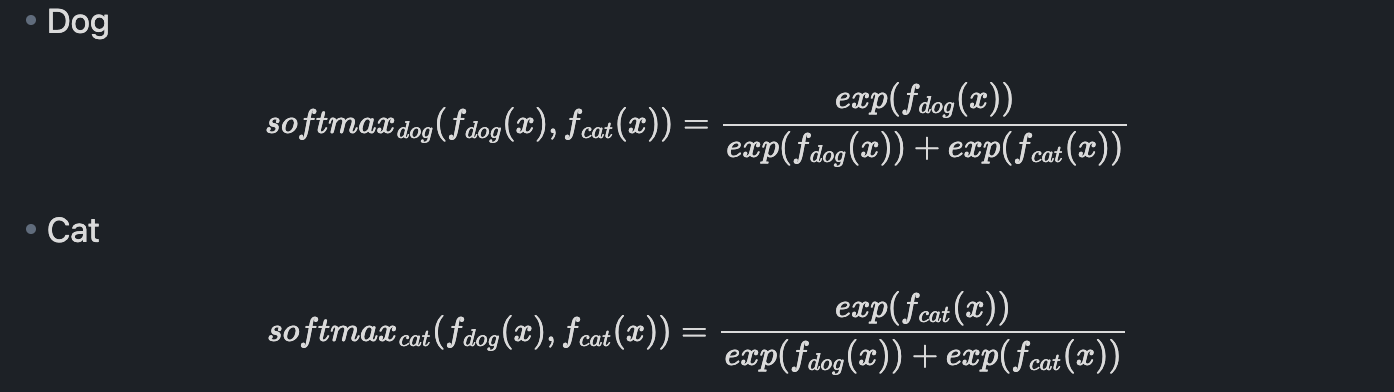
softmax function을 잘 살펴보면, 이전에 언급했던 내용을 볼 수 있습니다.

- "Nothing magical about softmax"
-"It's not the only way to do it, just need to get the numbers to be Positive and Sum to 1"

3. Loss Function
이제는 Loss function에 대해서 살펴보려고 합니다. 먼저 우리가 이전에 정의했던 함수를 다시 보면 다음과 같습니다.
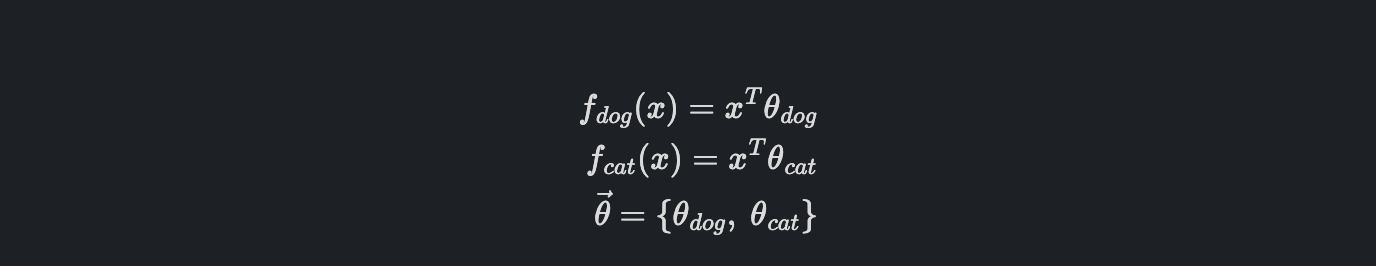
이제 어떻게 우리는 학습 파라미터를 어떻게 결정할지에 대해서 생각해 봅시다.
잠시 어떤 문제를 풀기 위한 formal 한 machine learning method에 대해서 살펴봅시다.

이러한 단계에서 2단계에 대해서 살펴보려고 하는 것입니다.
이를 살펴보기 위해서 dataset이 어떻게 만들어지는지부터 생각해 봅시다.
How is the dataset "generated"?
Random variable x는 어떤 분포 p(x)를 따를 것이고, 데이터셋은 p(x)로부터 random sampling으로 추출하여 사용합니다.
이를 우리는 이렇게 표현할 수 있습니다.
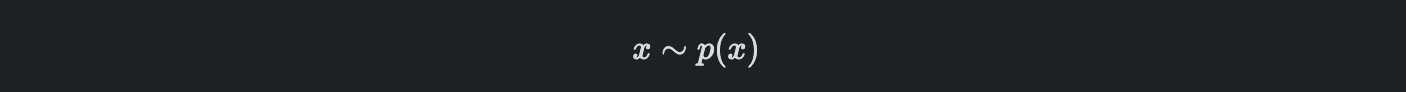
각 추출한 데이터의 labels들에 대한 conditional distribution이 만들어집니다.

결과적으로, chain rule에 의해서 x, y sample을 x, y의 joint distribution으로 표현할 수 있습니다.
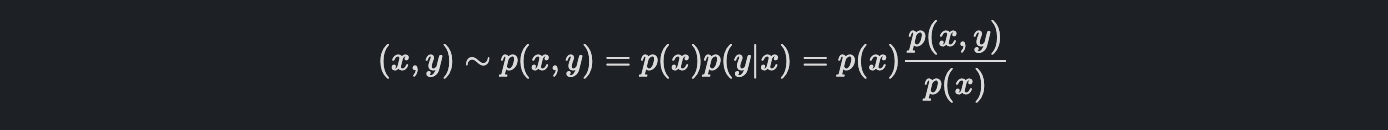
이렇게 놓고 보면, Dataset (x, y)는 x와 y의 joint distribution인 p(x, y)에서 샘플링된 것이라는 생각을 할 수 있습니다.
Training set

여기서 그러면 P(D)는 무엇이냐?라고 하면 i.i.d를 가정하고 있기 때문에, 다음과 같습니다.
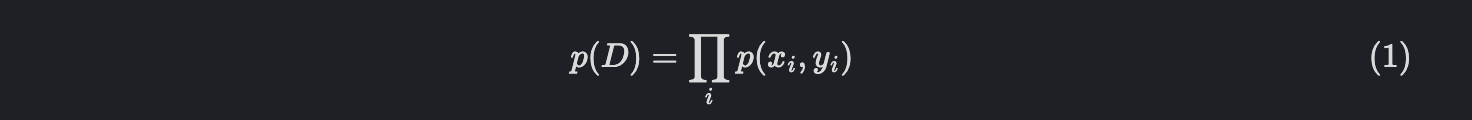

(1) 식을 다시 표현하면,
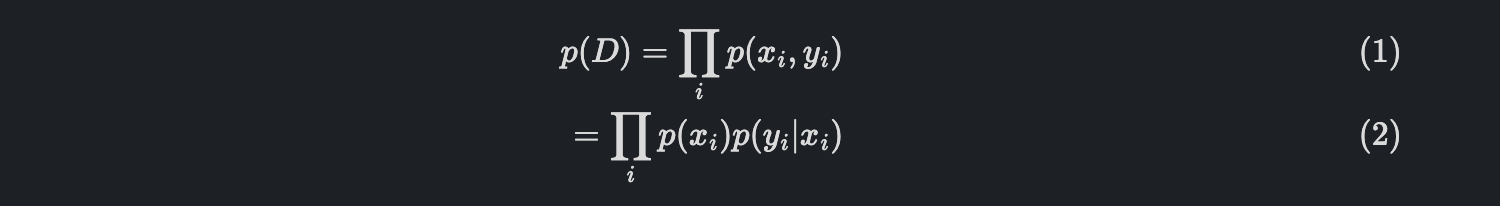
자 처음에 우리가 학습 파라미터를 가진 확률분포를 학습시킬 건데, 이는 결국에 True p(y|x)의 model이 되는 것입니다.
정리하자면,

따라서 파라미터를 정하는 아이디어로 다음과 같이 생각해 볼 수 있습니다.
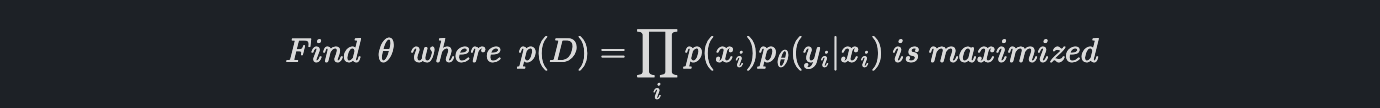
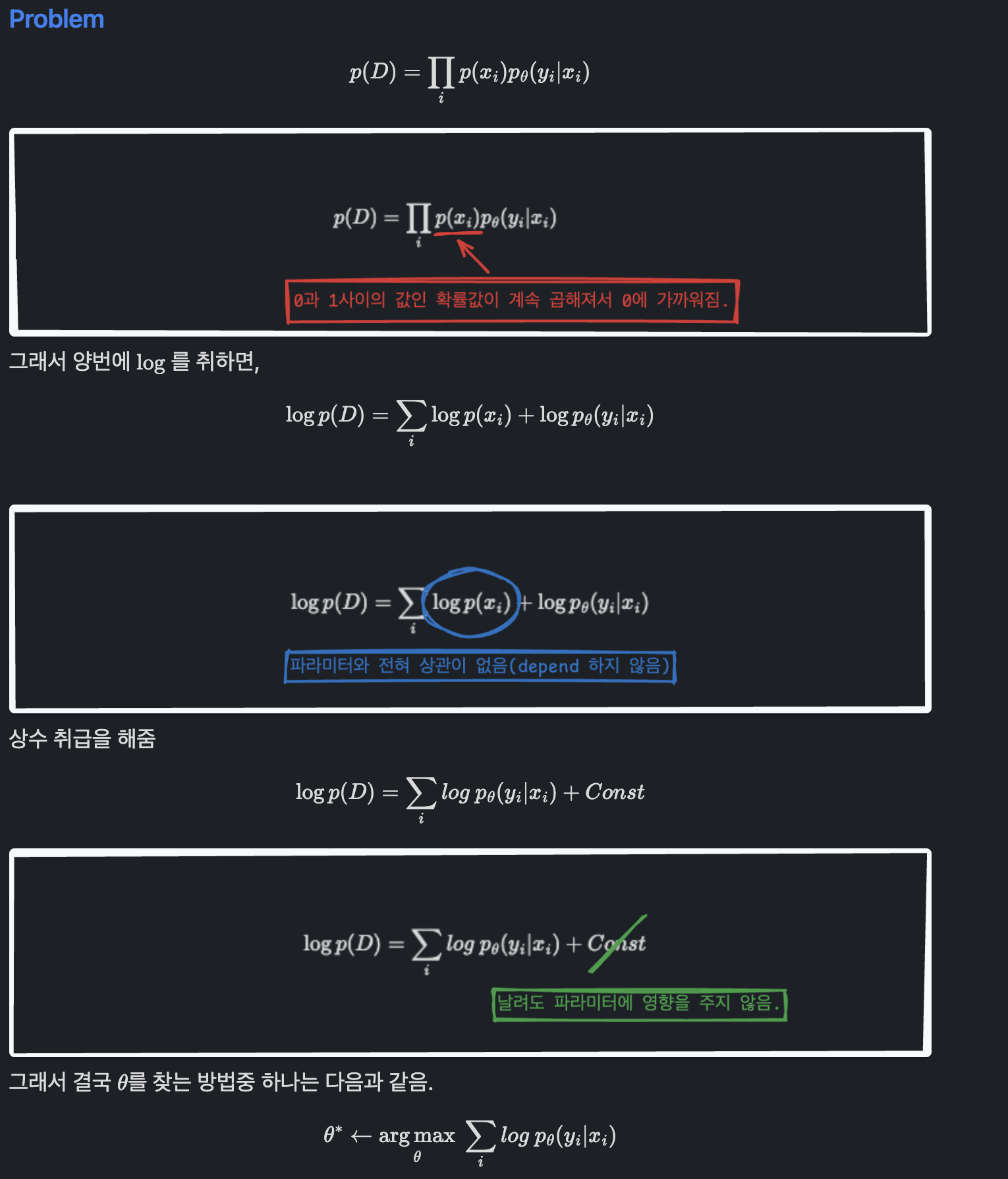
위 방법을 Maximum Likelihood Estimation(MLE)라고 합니다. 반대로 maximize 문제를 minimize문제로 바꾸면, 이를 Negative Log-Likelihood(NLL)이라고 하고 이것이 우리가 사용하는 Loss Function입니다.
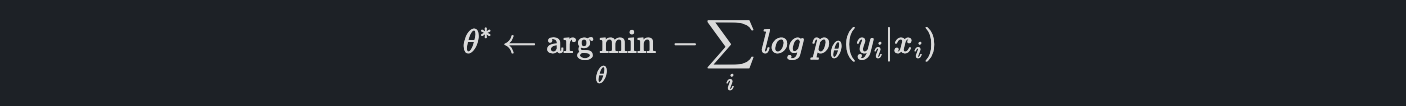
Example of Loss functions
- Negative log-likelihood (Cross-Entropy)
- Zero-one loss
- MSE(Actually just NLL)

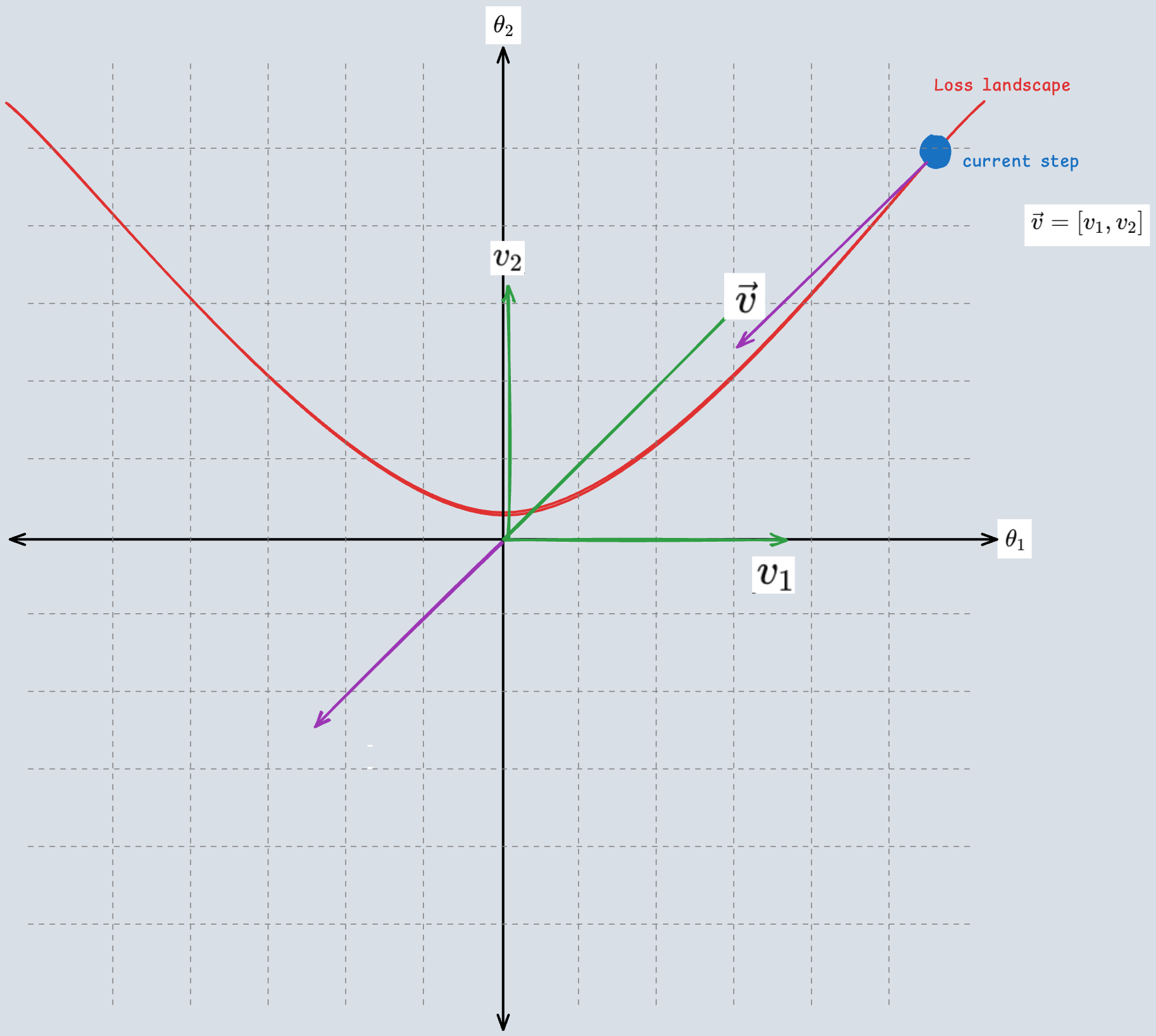
4. Optimization
지금까지 model class를 정의하고 loss function도 알아봤습니다. 이전에 정의했던 Loss function을 단순하게 이렇게 표현해 봅시다.

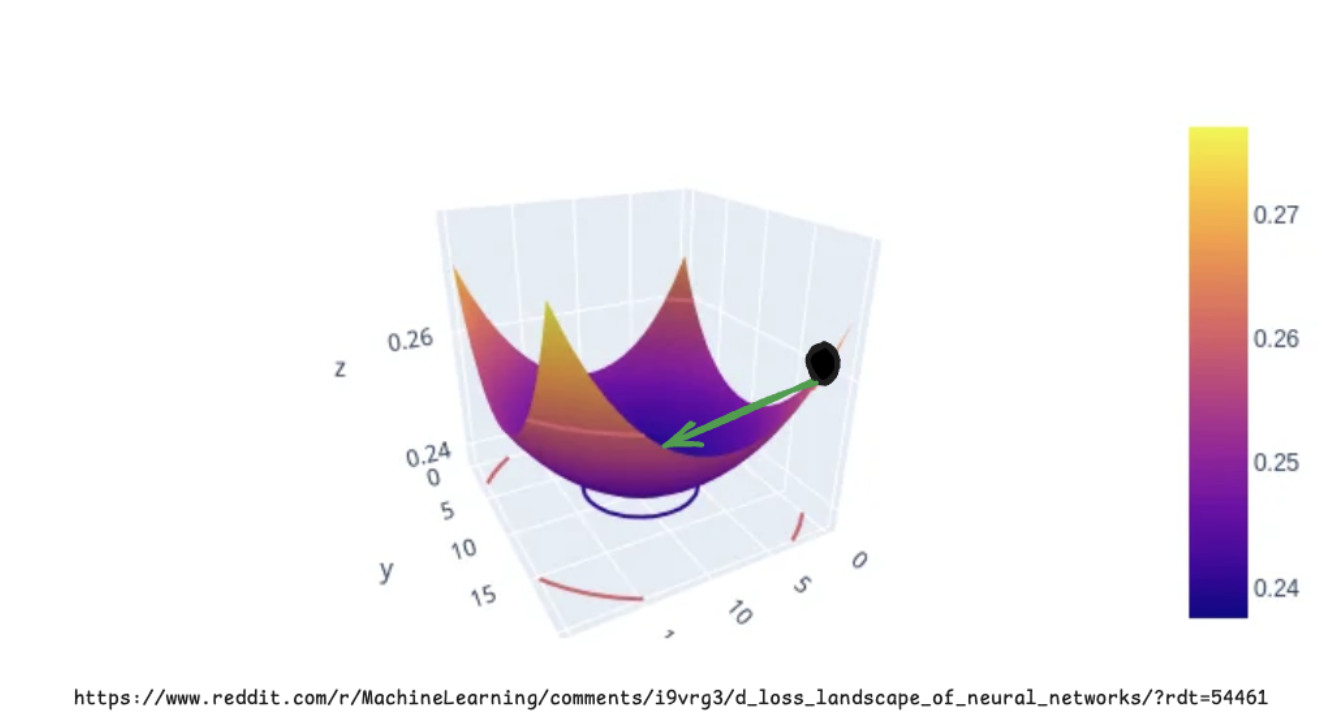
참 분포와 가까워지려면 loss가 최소인 상태로 가야 합니다. 이를 loss landscape 상에서 표현하면 위와 같이 표현할 수 있고, 검은색 포인트에서 화살표 방향으로 가야 하는 것입니다. (화살표 방향으로 가는 과정이 우리가 이야기하는 training)

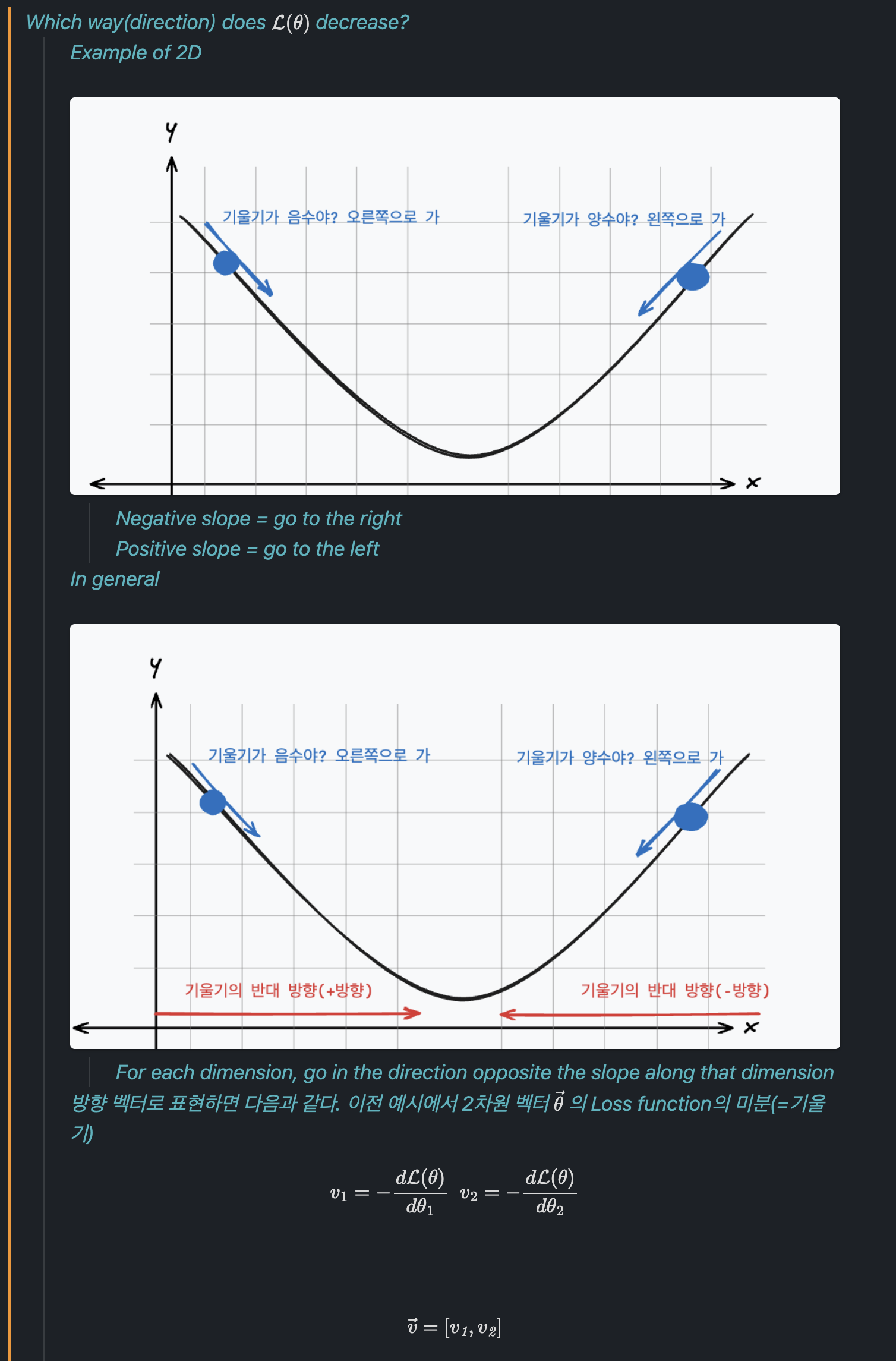

5. Risk
Loss function 그리고 optimization까지 살펴봤습니다. 이제는 Risk에 대해서 알아봅시다.
Risk는 다음과 같이 정의할 수 있습니다.
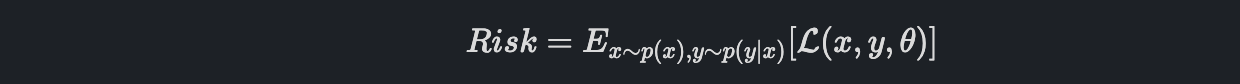
True 분포에 대한 loss의 기댓값입니다.

결과적으로 Supervised Learning이라고 하는 것은 Empirical Risk minimization이다.라고 정리할 수 있겠습니다.
'AI' 카테고리의 다른 글
| RNN, Sequence-to-Sequence model (0) | 2024.11.04 |
|---|---|
| 인공지능 기초 Optimization (0) | 2024.10.26 |
| Embodied AI : Vision-Language Navigation Challenges (3) | 2024.09.28 |
| Embodied AI : Survey(2) (3) | 2024.09.01 |
| Embodied AI : Next-Gen AI System(1) (2) | 2024.08.10 |




