| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- data discovery
- blockchain
- embodied ai
- bitcoin
- video understanding
- vision-language navigation
- 디스코드챗봇
- Ai
- embodied
- Rust
- crwaling
- MLFlow
- airflow
- ChatGPT
- databricks
- vln
- Spark
- GPT
- 블록체인
- frontend
- 디스코드봇
- Golang
- discord
- bricksassistant
- datahub
- backend
- Hexagonal Architecture
- 챗봇
- 디스코드
- s3
- Today
- Total
BRICKSTUDY
인공지능 기초 Optimization 본문
0. 개요
안녕하십니까, 브릭스터디 박찬영입니다. 최근 인공지능 관련 기초 개념들을 다시 복습하고 있는데요. 공유하기 좋은 내용이라고 생각해서 이번 포스팅을 작성합니다. 전체적인 복습은 https://cs182sp21.github.io/ (UC Berkeley CS W182)를 보면서 진행하고 있습니다. 전반적인 인공지능 필수 개념을 다루고 있어서 좋은 강의라고 생각합니다.
그래서 이번 포스팅에서 다룰 내용은 Optimization을 다루려고 합니다. 지난 인공지능 기초 포스팅에서 2024.10.11 - [AI] - Supervised Learning 기초 지도학습을 다루면서 gradient descent 방법까지 살펴봤었는데, 이번에는 Opimization 측면에서 살펴보도록 하겠습니다.
1. Gradient Descent
그냥 보기에는 잘 사용하고 있고, 좋은 알고리즘이라고 생각하지만, gradient descent 알고리즘도 문제점이 없는 것은 아닙니다. 해당 알고리즘의 문제점은 우리가 찾은 방향(direction)이 항상 좋은 방향이 아니라는 점입니다.
gradient descent 알고리즘은 항상 steepest descent direction을 취합니다. 하지만 steepest direction이 항상 minimum poin로 향하는 것이 아닙니다.
이해를 돕기 위해서 다음 그림을 생각해 볼 수 있습니다.

빨간색 점인, start point에서 초록색 점 optimum으로 가야 할 때, 최적의 동선은 주황색 화살표가 될 것입니다. 그러나, steepest direction을 취하게 되면 빨간색 화살표처럼 돌아가는 길을 선택하게 됩니다.
이 문제를 살펴보기 전에 convexity에 대해서 간단하게 알아보도록 합시다.
2. Convex Function

어떤 함수가 convex 하다는 것은, 그 함수 그래프 상의 두 점을 잇는 직선 구간이 항상 함수 그래프 위쪽에 위치하는 것을 의미합니다.
쉽게 말해서 두 점 사이을 직선으로 연결했을 때, 그 직선이 함수 곡선의 아래로 내려가지 않으면 그 함수는 convex 하다고 할 수 있는 것입니다. convex 함수는 gradient descent와 같은 단순한 알고리즘도 최적값에 쉽게 도달할 수 있습니다.(convex function에서는 local minimum이 global minimum이 되기 때문)
대표적으로 logistic regression에서 Negative likelihood loss는 convex 합니다.
Convex function은 최적값을 찾기 쉽다! 고 기억하면 될 것입니다. 자 그럼 이제 우리가 보통 최적화를 해야 하는 loss에 대한 surface를 한 번 살펴봅시다.
The Loss surface of a neural network
우선은 Neural network의 loss landscape를 visualize 하는 작업은 매우 매우 어려운 작업입니다. 모든 조합의 parameter를 다 계산해야 하기 때문인데, neural network는 알다시피 파라미터 개수가 매우 많기 때문입니다.
그런데, 논문 Li, Hao, et al. "Visualizing the loss landscape of neural nets." Advances in neural information processing systems 31 (2018). 에서 우리가 잘 알고 있는 유명한 네트워크인 ResNet의 loss landscape를 시각화를 했습니다.

(a)를 보면 엄청난 수준의 협곡들이 존재합니다. 각 협곡의 아래가 local optima가 된다고 생각하면 될 것 같습니다.
Local opima
Local optima 문제는 많은 사람들이 Neural net에 대해서 걱정하는 이유 중 하나이고, non-convex function optimization의 대표적인 문제입니다.
!
파라미터 수가 증가할수록 (즉, 네트워크가 커질수록) 이런 문제가 덜 심각해진다. 큰 네트워크에서는 local optima가 존재하지만, 이러한 값들이 global optima와 크게 차이가 나지 않는 경향이 있다고 한다. 즉, gradient descent로 도달한 local optima라고 해도 global optima에 매우 가까운 좋은 값일 가능성이 높다.
local optima에 빠지기 쉽거나, 학습을 방해하는 지형 유형에 대해서 간단하게 2가지 정도 살펴보도록 하겠습니다.
Plateaus
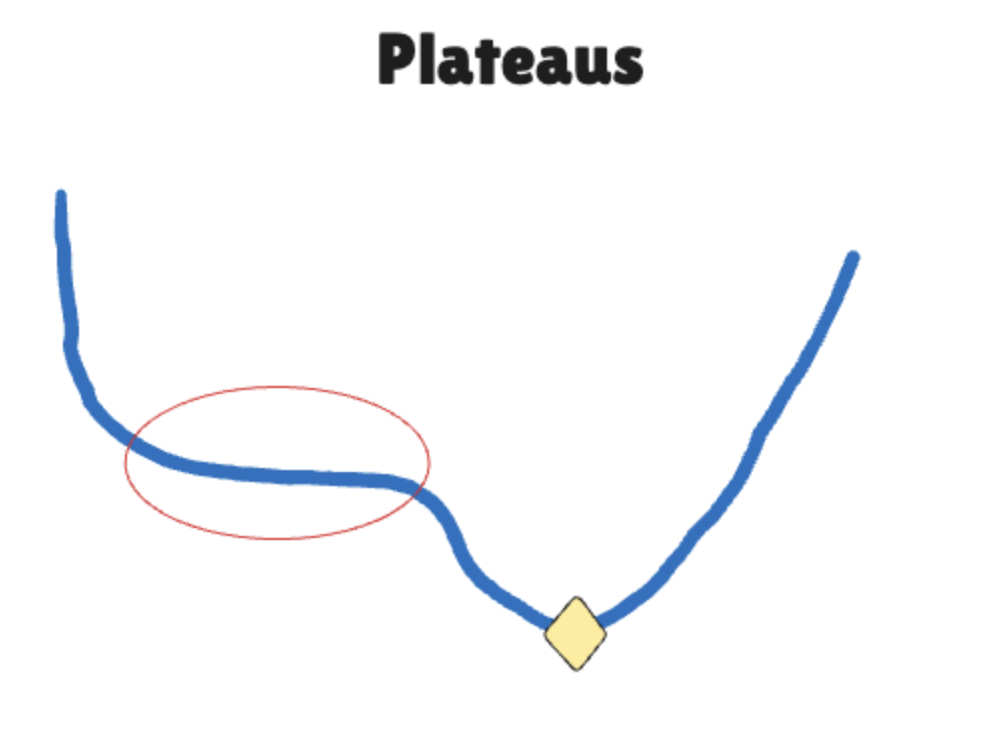
학습을 하다 보면, 저렇게 평탄한 구간에 갇힐 수가 있습니다. 평탄한 구간이라서 gradient값이 매우 작기 때문에 쉽게 빠져나가지 못하는 것도 있습니다. 그래서 평탄한 구간에서는 learning rate 값이 충분히 커야 빠르게 진행될 수가 있습니다.
Saddle point(안장점)
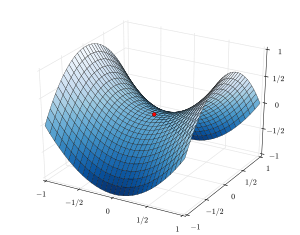
안장점에서는 gradient가 0이기 때문에 학습이 어렵습니다. 어떤 방향에서는 기울기가 양수이고, 어떤 방향에서는 기울기가 음수이기 때문에 진동하거나 방향을 잃을 수가 있습니다.
엄청나게 특이한 구조라고 생각하지만, neural network에서의 critical point의 대부분은 saddle point입니다.
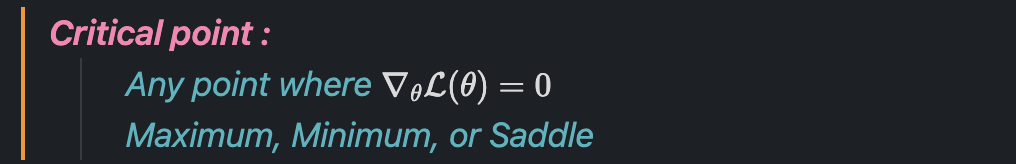


여기서 Hessian matrix의 diagonal entries들이 모두 양수이면, 해당 지점은 minimum이고, 모두 음수이면, 해당 지점은 maximum에 해당하는데, 고차원에서는 entries가 매우 많기 때문에, 대각 원소들이 모두 같은 부호일 확률이 매우 낮습니다. 결과적으로 양수와 음수가 섞이기 쉽고, 이는 minimum이나, maximum이 아니라 saddle point가 됩니다. 따라서 대부분의 고차원 neural network의 critical point는 saddle point입니다.
3. Improvement direction
자 그래서 어떻게 쉽게 최적화할 것인가?를 생각해 봅시다.
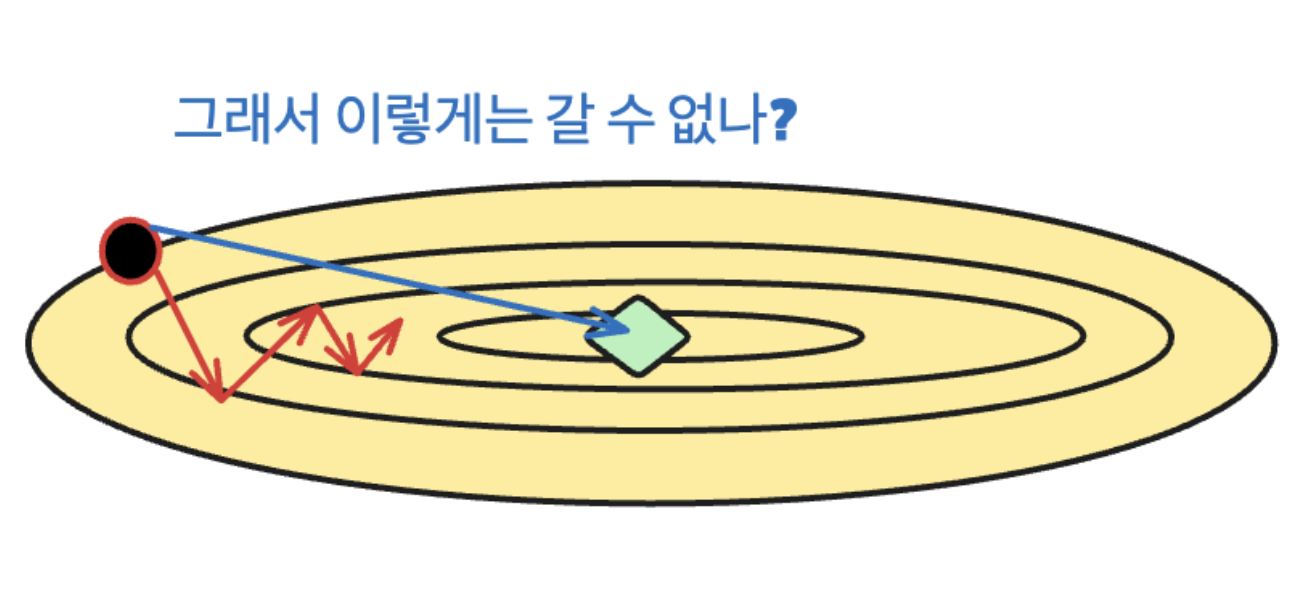
Momentum
첫 번째로 살펴볼 방식은 모멘텀입니다. 모멘텀의 경우에는 직관적으로는 여러 번 갈 거 한 번에 가자는 느낌인데요
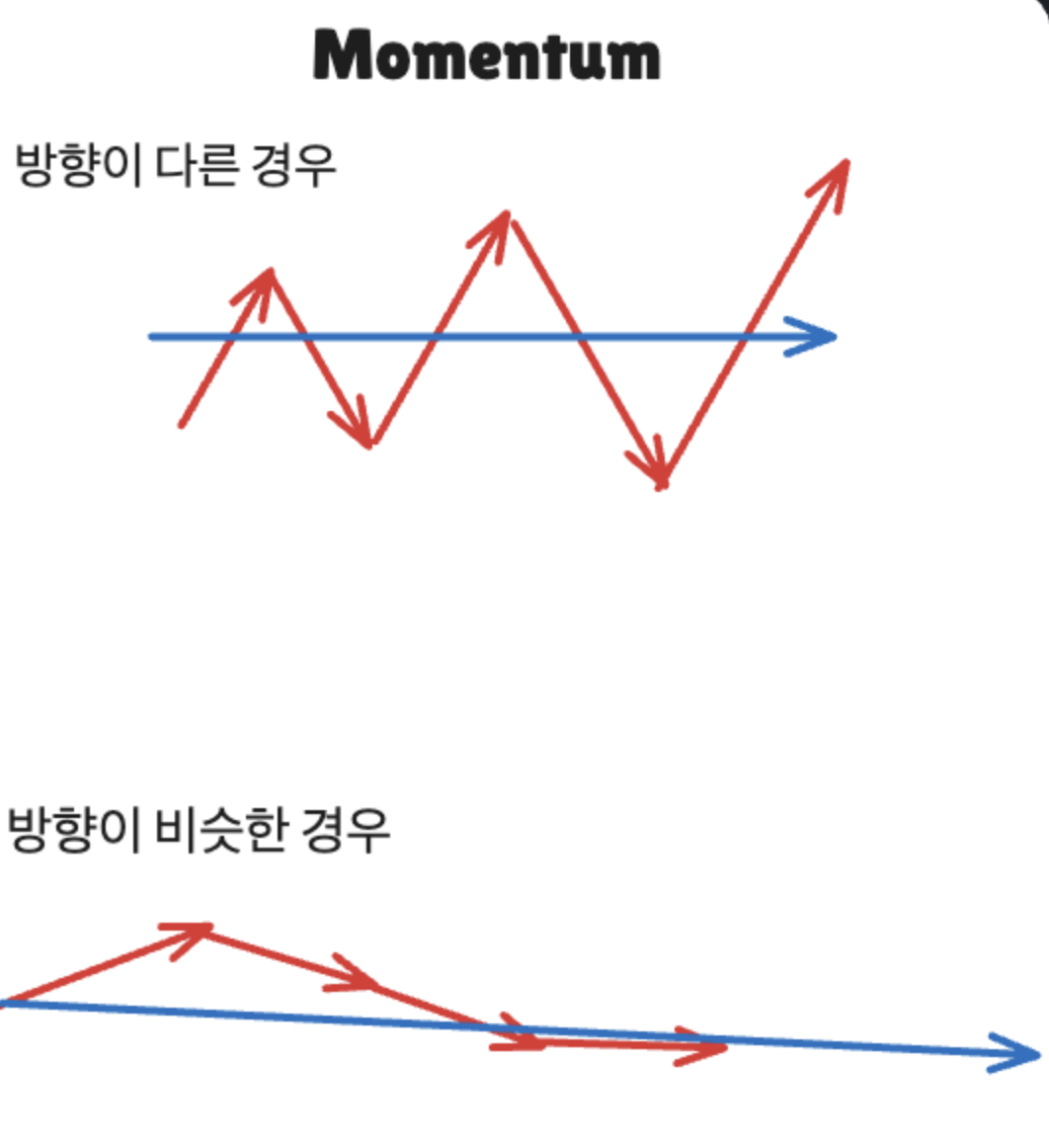
Gradient step이 다른 방향으로 계속 이어지면, 몇 개의 해당하는 step을 모아서 방향의 평균 방향으로 가는 방법이 있을 수 있겠고, 서로 방향이 비슷하게 이어지면, 조금씩 가는 것이 아니라 해당 방향으로 빠르게 가는 방법이 있습니다.

Newton's method
뉴턴 방법은 2차 테일러 전개를 사용해서 현재 위치에서 함수가 최소가 될 것으로 예상되는 지점을 찾는 방법입니다. 뉴턴 방법에서는 2차 미분 정보까지 활용해서 더 정확하게 방향과 크기를 예측할 수 있습니다.
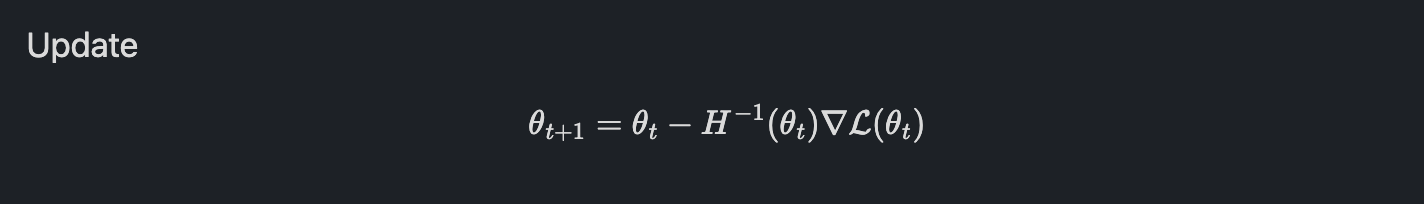
직관적으로 뉴턴방법은 곡률정보(2차 미분, Hessian matrix)를 사용해 얼마나 크게 이동해야 할지를 계산하는 것입니다.
> 만약 함수가 매우 가파르다면, 적게 이동하고
> 함수가 평평하다면 더 멀리 이동하는
그러나 뉴턴 방법은 Hessian matrix를 연산해야 하는 문제 때문에 실제로는 너무 cost가 비싸서 잘 사용하지 않습니다.
4. Algorithms
기울기의 부호는 각 차원에서 어느 방향으로 이동해야 하는지를 알려주지만, 기울기의 크기(Magnitude)는 불안정할 수 있습니다.
특히 최악의 경우, 최적화 과정에서 기울기 크기가 극단적으로 변할 수 있어서, learning rate를 적절하게 조절하는 것이 어렵습니다.
예를 들어 초기에는 큰 기울기가 발생해 빠르게 학습해야 하지만, 후반부에는 기울기가 작아져 더 작은 learning rate가 필요할 수 있고
이에 대한 아이디어로, "각 차원에 대해서 기울기의 magnitude를 normalize 하자"라는 것입니다.
RMSProp(Root Mean Square Propagation)
Estimate per-dimension magnitude (running average)

AdaGrad
Estimate per-dimension cumulative magnitude

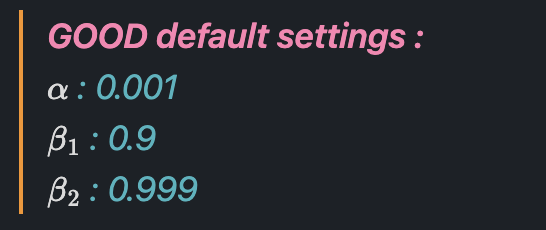
Adam
Basic Idea : combine momentum and RMSProp

5. Learning rate
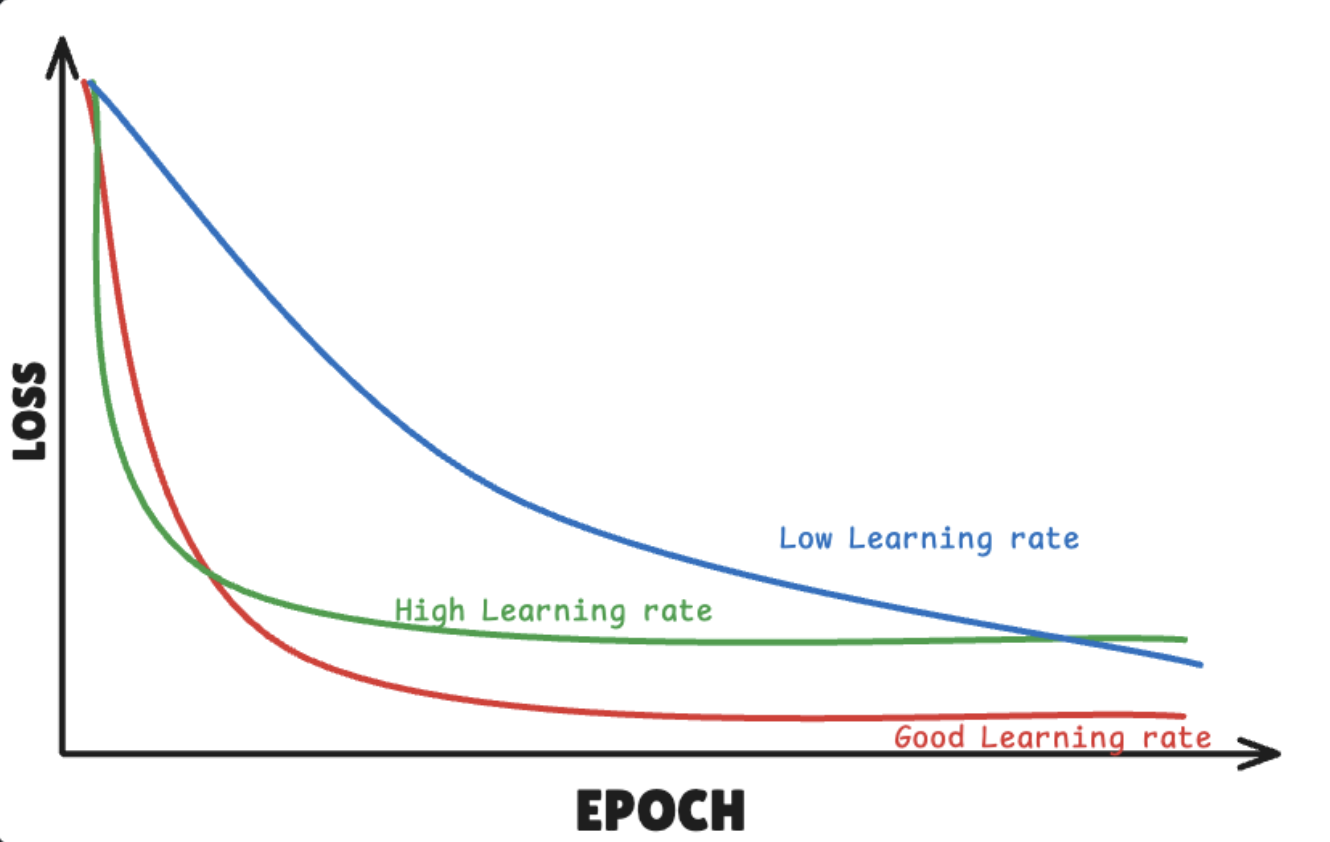
Decaying learning rate
learning rate를 점점 작게 만드는 기법
learning rate decay schedules usually needed for best performance with SGD
often not needed with ADAM
'AI' 카테고리의 다른 글
| Attention, Transformer를 알아보자 (0) | 2024.11.05 |
|---|---|
| RNN, Sequence-to-Sequence model (0) | 2024.11.04 |
| Supervised Learning 기초 (6) | 2024.10.11 |
| Embodied AI : Vision-Language Navigation Challenges (3) | 2024.09.28 |
| Embodied AI : Survey(2) (3) | 2024.09.01 |





